Integrator II - Untersummen- und Obersummenfunktionen, Integralfunktion
Statt auf dem Intervall [a; b] zu rechnen, kann man das auch dynamisieren,
indem man mit variablem x aus [a; b] auf dem Intervall [a; x] integriert.
Nimmt man an der Stelle x = x(S) die Werte der Untersumme bzw. Obersumme über [a; x] als y-Koordinate eines Punktes, so erhält man Punkte Ua und Oa. Diese sind in der Regel bei kleinem n unterschiedlich und kommen bei integrierbaren Funktionen f für größeres n immer näher zusammen.
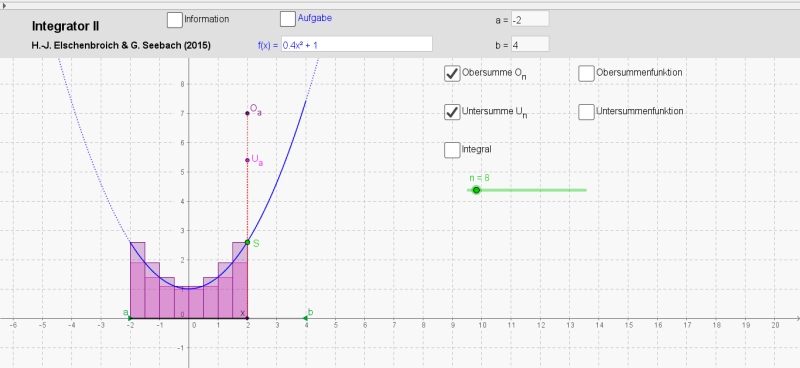
Integrator II für n = 8
Diese
Punkte Ua und Oa bewegen sich, wenn man an S zieht
(man hätte das auch mit Ziehen an x realisieren können). Deswegen können sie eine Ortslinie
erzeugen, den Graphen der Untersummenfunktion Ua(x) bzw. Obersummenfunktion
Oa(x). Die linke Grenze a spielt dabei neben dem n als Parameter eine wichtige
Rolle, denn hier starten die Funktionen mit dem Wert 0.
Wenn man es genau nimmt, müsste man eigentlich Ua,n(x)
schreiben. Dies ist aber für die Schule unüblich komplex und da der
Zusammenhang mit n hoffentlich intuitiv klar ist, habe ich darauf
verzichtet.
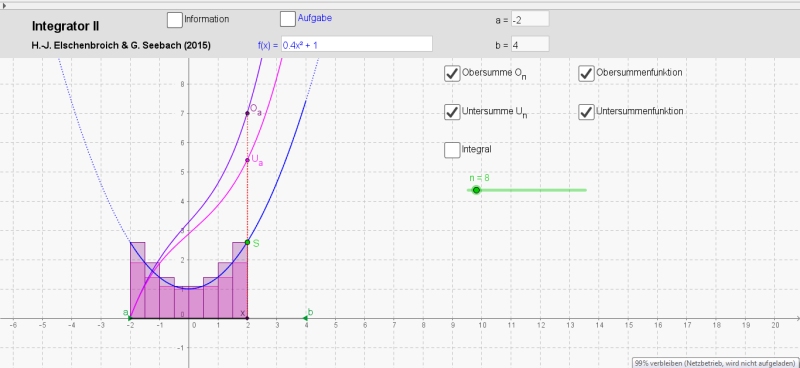
Integrator II für n = 8 mit Untersummenfunktion Ua(x) und Obersummenfunktion Oa(x)
Wird jetzt n vergrößert, so nähern sich bei einer integrierbaren Funktion f diese beiden Graphen immer mehr an und fallen schließlich ununterscheidbar zusammen. Dann ist dann der Graph der Integralfunktion.
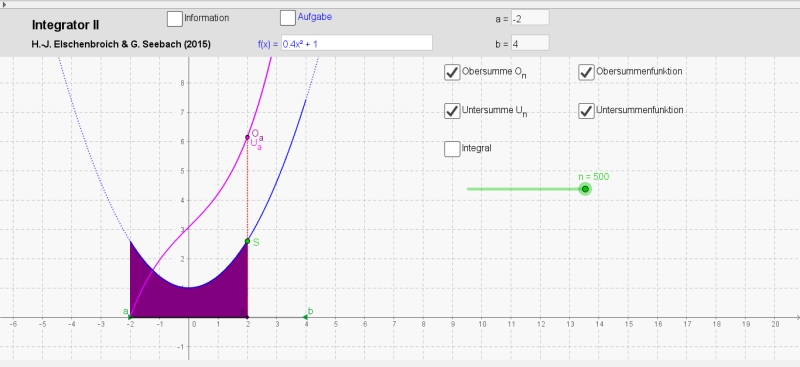
Integrator II für n = 1000 mit Untersummenfunktion Ua(x) und Obersummenfunktion Oa(x)
Auch hier haben wir einen auf der Nutzerebene kalkülfreien Zugang. Die Software berechnet die jeweiligen Werte und erzeugt aus den Punkten die Ortslinien (was durchaus zeitaufwändig werden kann), die dann als Funktionsgraphen gedeutet und untersucht werden können. Wir haben einen graphischen Zugang zu Untersummenfunktion, Obersummenfunktion und Integralfunktion, ohne dass wir dafür deren Funktionsterme kennen und und nutzen.
Dieser
Weg über die Untersummenfunktion Ua(x) und Obersummenfunktion
Oa(x) ist interessant und ein schönes Beispiel für funktionalen
Zusammenhang. Und er zeigt eine Parallele zu den Sekantensteigungenfunktionen
bei der Differenzialrechnung. Aber er ist auch anspruchsvoll und eher für einen Leistungskurs
geeignet. Natürlich kann man, nachdem in Integrator I der Zusammenhang von
Untersummen, Obersummen und Integral untersucht wurde, auch direkt zur
Integralfunktion übergehen (siehe Integrator III).